Post by kellyyu on Apr 7, 2024 4:13:41 GMT -5
Compared with the traditional gyro, MEMS gyroscope has the advantages of small size, light weight, easy integration, etc. MEMS is short for Micro Electro Mechanical Systems. MEMS gyro sensor has a wide application prospect in military and civilian fields such as weapon navigation and vehicle navigation. Nowadays, its application in the civil field is more and more extensive, MEMS gyro in oil logging, mining, directional drilling, aerospace, mapping and other fields can play an important role.
Even with precision instruments, there are errors. The error of MEMS gyroscopes mainly includes two parts: deterministic error and random error, which are composed of zero error and installation error. Deterministic error is regular, and the value can be determined by test method. Random errors are irregular errors caused by changes in gyroscope operating environment, bearing noise and temperature, which cannot be compensated by simple methods. Signal denoising is a way to compensate the error of MEMS gyro. This paper will introduce the principle and evaluation index of MEMS gyroscope signal denoising.
Signal denoising principle of MEMS gyroscope
Wavelet analysis is widely used in signal processing, and signal denoising is an important application of wavelet analysis.
Let s(t) with noise be represented as:
Where: ƒ(t) is a real signal, e(t) is a Gaussian white noise signal.
Under normal circumstances, the real signal is generally a lower frequency or a more stable signal, and the noise is generally distributed in the high frequency part, and its change is very drastic. The signal denoising processing is to weaken the noise in the signal, so as to extract the real signal. There are usually three main steps for signal denoising processing:
(1) Select the best wavelet basis function and decomposition scale N for wavelet decomposition of the signal.
(2) Set a threshold to quantify the decomposed high-frequency coefficient threshold.
(3) Wavelet reconstruction is carried out between the decomposed low frequency coefficient and the processed high frequency coefficient.
After the above three steps, the signal is denoised by wavelet. The effect of denoising mainly depends on the selection of threshold and how to quantize the signal threshold.
In practical applications, the signal is usually a non-stationary white noise signal, with many spikes and mutations, which makes it difficult to accurately analyze and process the signal. Usually, the noise contained in the signal must be weakened first to obtain useful signals. The traditional Fourier method can not analyze the signal in the time domain, but can only analyze the signal roughly in the frequency domain, and can not get the detailed analysis of the signal at a certain point in time, it is difficult to distinguish the signal mutation part from the noise, which makes the Fourier analysis method to the non-stationary signal analysis is greatly limited. The wavelet analysis method can analyze the signal carefully in both time and frequency domains, identify the abrupt part and noise in the signal, and achieve good results in the analysis and processing of non-stationary signals.
The random error of MEMS gyroscope is weak linear, non-stationary, and has great drift. The traditional methods such as Fourier analysis and Kalman filtering can not get the desired analysis results and the best denoising effect. The wavelet analysis method can well analyze and process non-stationary and nonlinear signals, so this paper adopts the wavelet analysis method to analyze and process the random error signal of MEMS gyroscope.
The evaluation index of signal denoising
In order to more clearly select the appropriate denoising method and wavelet basis function for MEMS gyro random error signal analysis and processing, it is necessary to select some evaluation indicators. By analyzing and comparing the evaluation indicators, the appropriate denoising method and wavelet basis function can be selected. In this way, better results can be obtained when analyzing and processing random error signals of MEMS gyroscope.
Some evaluation indexes usually used in the analysis and processing of signals include mean value, standard deviation and signal-to-noise ratio. When using wavelet denoising method to denoise MEMS gyros random error signal, the smaller the difference between the signal mean after denoising and the mean of the original signal, the better. The smaller the signal standard deviation after denoising, the more stable the MEMS gyroscope random error signal after denoising, and the larger the signal-to-noise ratio after denoising, the better the denoising effect. The mathematical expression of each index is as follows:
Average:
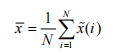
Where, N is the signal length, and x(i) is the signal after denoising.
Standard deviation:
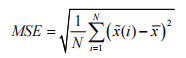
Where N is the signal length, x is the mean value of the signal after de-noising, and x(i) is the signal after de-noising.
Signal to noise ratio:
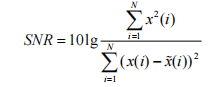
Where N is the signal length, x(i) is the original signal, and x(i) is the signal after denoising.
By comparing the above three evaluation indexes, the appropriate denoising method and wavelet basis function can be selected, so that the random error signal of MEMS gyroscope can be better analyzed and processed.
Conclusion
This paper introduces the signal denoising principle and evaluation index of MEMS gyro. MEMS gyro as a precision instrument, there will inevitably be errors, this error may be caused by environmental reasons, may also be due to their own reasons, so the error compensation is an important step to improve the accuracy of MEMS gyroscopes. Ericco conducts rigorous calibration and error compensation for MEMS gyroscopes, focusing on the production and development of navigational and tactical MEMS gyroscopes. For example, the ER-MG2-50/100 is a navigation-grade north finding MEMS gyroscope, while the ER-MG-068 is a tactical grade high-precision MEMS gyro.
If you are interested in learning more about MEMS gyro, please contact us.
Even with precision instruments, there are errors. The error of MEMS gyroscopes mainly includes two parts: deterministic error and random error, which are composed of zero error and installation error. Deterministic error is regular, and the value can be determined by test method. Random errors are irregular errors caused by changes in gyroscope operating environment, bearing noise and temperature, which cannot be compensated by simple methods. Signal denoising is a way to compensate the error of MEMS gyro. This paper will introduce the principle and evaluation index of MEMS gyroscope signal denoising.
Signal denoising principle of MEMS gyroscope
Wavelet analysis is widely used in signal processing, and signal denoising is an important application of wavelet analysis.
Let s(t) with noise be represented as:
s(t)=ƒ(t)+εe(t)
Where: ƒ(t) is a real signal, e(t) is a Gaussian white noise signal.
Under normal circumstances, the real signal is generally a lower frequency or a more stable signal, and the noise is generally distributed in the high frequency part, and its change is very drastic. The signal denoising processing is to weaken the noise in the signal, so as to extract the real signal. There are usually three main steps for signal denoising processing:
(1) Select the best wavelet basis function and decomposition scale N for wavelet decomposition of the signal.
(2) Set a threshold to quantify the decomposed high-frequency coefficient threshold.
(3) Wavelet reconstruction is carried out between the decomposed low frequency coefficient and the processed high frequency coefficient.
After the above three steps, the signal is denoised by wavelet. The effect of denoising mainly depends on the selection of threshold and how to quantize the signal threshold.
In practical applications, the signal is usually a non-stationary white noise signal, with many spikes and mutations, which makes it difficult to accurately analyze and process the signal. Usually, the noise contained in the signal must be weakened first to obtain useful signals. The traditional Fourier method can not analyze the signal in the time domain, but can only analyze the signal roughly in the frequency domain, and can not get the detailed analysis of the signal at a certain point in time, it is difficult to distinguish the signal mutation part from the noise, which makes the Fourier analysis method to the non-stationary signal analysis is greatly limited. The wavelet analysis method can analyze the signal carefully in both time and frequency domains, identify the abrupt part and noise in the signal, and achieve good results in the analysis and processing of non-stationary signals.
The random error of MEMS gyroscope is weak linear, non-stationary, and has great drift. The traditional methods such as Fourier analysis and Kalman filtering can not get the desired analysis results and the best denoising effect. The wavelet analysis method can well analyze and process non-stationary and nonlinear signals, so this paper adopts the wavelet analysis method to analyze and process the random error signal of MEMS gyroscope.
The evaluation index of signal denoising
In order to more clearly select the appropriate denoising method and wavelet basis function for MEMS gyro random error signal analysis and processing, it is necessary to select some evaluation indicators. By analyzing and comparing the evaluation indicators, the appropriate denoising method and wavelet basis function can be selected. In this way, better results can be obtained when analyzing and processing random error signals of MEMS gyroscope.
Some evaluation indexes usually used in the analysis and processing of signals include mean value, standard deviation and signal-to-noise ratio. When using wavelet denoising method to denoise MEMS gyros random error signal, the smaller the difference between the signal mean after denoising and the mean of the original signal, the better. The smaller the signal standard deviation after denoising, the more stable the MEMS gyroscope random error signal after denoising, and the larger the signal-to-noise ratio after denoising, the better the denoising effect. The mathematical expression of each index is as follows:
Average:
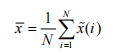
Where, N is the signal length, and x(i) is the signal after denoising.
Standard deviation:
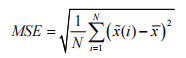
Where N is the signal length, x is the mean value of the signal after de-noising, and x(i) is the signal after de-noising.
Signal to noise ratio:
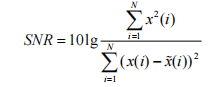
Where N is the signal length, x(i) is the original signal, and x(i) is the signal after denoising.
By comparing the above three evaluation indexes, the appropriate denoising method and wavelet basis function can be selected, so that the random error signal of MEMS gyroscope can be better analyzed and processed.
Conclusion
This paper introduces the signal denoising principle and evaluation index of MEMS gyro. MEMS gyro as a precision instrument, there will inevitably be errors, this error may be caused by environmental reasons, may also be due to their own reasons, so the error compensation is an important step to improve the accuracy of MEMS gyroscopes. Ericco conducts rigorous calibration and error compensation for MEMS gyroscopes, focusing on the production and development of navigational and tactical MEMS gyroscopes. For example, the ER-MG2-50/100 is a navigation-grade north finding MEMS gyroscope, while the ER-MG-068 is a tactical grade high-precision MEMS gyro.
If you are interested in learning more about MEMS gyro, please contact us.
