Post by kellyyu on Mar 18, 2024 4:16:34 GMT -5
MEMS gyroscope is the core component of inertial navigation system, it can play an important role in oil logging, drilling, aerospace, mining and mapping and other fields. Today, MEMS sensor can occupy a place in the industry, and more and more companies and manufacturers are willing to choose smaller size, lower cost, but excellent performance MEMS sensor.
MEMS gyroscope is the object that rotates at high speed around the rotational symmetry axis, the rotational symmetry axis is usually called the main axis of the gyroscope rotor, the common gyroscope is the high-speed rotating rotor, and the rotation of the rotor around the spindle is called the gyroscope rotation. The high-speed rotating gyroscope is installed by different means, so that the gyroscope spindle has one or two degrees of freedom of rotation in space, which constitutes a gyroscope. The main feature of MEMS gyroscope are precession and axial rigidity. Using these two features, some inertial instruments can be made, which can provide a variety of attitude information for the carrier, including angle, angular velocity and angular displacement.
Precession
When the MEMS gyroscope rotor rotates at a high speed and the X-axis has angular momentum, if a downward force F is applied to one end of the rotor to produce a constant moment MY in the direction of the horizontal axis Y, it seems that the spindle X should move down in the direction of the external force F, that is, it moves around the Y axis, but it is not the case, but the rotation of the chasing external moment MY around the Z axis. Similarly, a horizontal force acting on the Y-axis will produce an external moment MZ along the vertical Y-axis, and the main axis will rotate around the Y-axis in pursuit of the external moment MZ. In short, if the external torque acts along the horizontal Y-axis, the gyro main axis moves around the z-axis; If the external torque acts along the vertical Z axis, the gyro principal axis rotates around the Y axis. This motion is called the precession of the gyroscope; The characteristic that the angular momentum H tries to get closer to the external torque M in the shortest path under the action of the external torque is called the precession of the gyroscope.
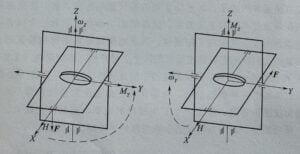
If the main shaft of the gyroscope is precession at angular velocity ω under the action of external torque M, the terminal linear velocity of the angular momentum vector H is:
According to the moment of momentum theorem, the angular momentum H vector terminal velocity v should be equal to the added external moment M, the expression is:
If the three are perpendicular to each other, the formula can be written as:
To wit:
It can be seen that under the action of the external torque, the main axis of the gyroscope will produce precession, and the precession direction is determined by the right hand rule. The precession angular velocity is proportional to the external torque and inversely proportional to the angular momentum. Among them, only the external torque component that is perpendicular to the angular momentum H can cause the precession of the gyroscope, and the precession of the gyroscope immediately occurs when the external torque is added to the gyroscope, and the precession of the gyroscope immediately stops when the external torque is removed. Therefore, it can be considered that the precession of the gyroscope is "inertially free". The precession of the gyroscope is based on Newton's theorem. Therefore, the rate of change of the angular momentum of the gyroscope under the action of the external torque is the rate of change of the relative inertial space, so the precession of the main shaft of the gyroscope is relative to the inertial space and is an absolute motion.
Axial rigidity
When the MEMS gyroscope rotor rotates at high speed with angular momentum, if there is no external torque, no matter how the base tilts or wobbles, its main shaft will always remain in the original direction, which is called the fixed axis of the gyroscope. Even if the sudden impact can be understood as giving the gyroscope a moment of impulse, the spindle still remains in the original spatial orientation, which is the nutation of the gyroscope. This impact resistance of the gyroscope is the stability of the gyroscope. The moment of momentum theorem for the axiality of a gyroscope can be understood as saying that if the external moment acting on the gyroscope is zero, then the velocity at the end of the angular momentum is also zero.
It follows that angular momentum changes neither magnitude nor direction in inertial space. Because the direction of angular momentum is consistent with the main axis of the gyroscope, if the main axis always points to a certain direction in space, it will always point to that direction in the future, which is why the gyroscope has a fixed axis. Its stability can also be determined by using the moment of momentum theorem.
Since the moment M is the effect of the pulse, dt approaches zero, so dH also approaches zero, indicating that there is no significant change in angular momentum, that is, the gyroscope spindle will keep the original direction unchanged. It is found through experiments that the greater the angular momentum, the better the stability of the gyroscope.
Conclusion
Through this article, we have learned two characteristics of MEMS gyroscope, through which it can play a role. Ericco specializes in the development of one -, two - and three-axis MEMS gyroscopes. For example, ER-MG2-50/100 has bias instability of 0.01 to 0.02°/hr and angular random walks of 0.0025 to 0.005°/√hr. The ER-2MG-06 is a high-performance two-axis MEMS gyroscope with bias instability of 0.1º/h. The ER-3MG-301 is a high-precision three-axis MEMS gyroscope whose main features are miniaturization and low power consumption.
If you are interested in MEMS gyro, please contact us.
MEMS gyroscope is the object that rotates at high speed around the rotational symmetry axis, the rotational symmetry axis is usually called the main axis of the gyroscope rotor, the common gyroscope is the high-speed rotating rotor, and the rotation of the rotor around the spindle is called the gyroscope rotation. The high-speed rotating gyroscope is installed by different means, so that the gyroscope spindle has one or two degrees of freedom of rotation in space, which constitutes a gyroscope. The main feature of MEMS gyroscope are precession and axial rigidity. Using these two features, some inertial instruments can be made, which can provide a variety of attitude information for the carrier, including angle, angular velocity and angular displacement.
Precession
When the MEMS gyroscope rotor rotates at a high speed and the X-axis has angular momentum, if a downward force F is applied to one end of the rotor to produce a constant moment MY in the direction of the horizontal axis Y, it seems that the spindle X should move down in the direction of the external force F, that is, it moves around the Y axis, but it is not the case, but the rotation of the chasing external moment MY around the Z axis. Similarly, a horizontal force acting on the Y-axis will produce an external moment MZ along the vertical Y-axis, and the main axis will rotate around the Y-axis in pursuit of the external moment MZ. In short, if the external torque acts along the horizontal Y-axis, the gyro main axis moves around the z-axis; If the external torque acts along the vertical Z axis, the gyro principal axis rotates around the Y axis. This motion is called the precession of the gyroscope; The characteristic that the angular momentum H tries to get closer to the external torque M in the shortest path under the action of the external torque is called the precession of the gyroscope.

Figure 1 Precession of a gyroscope
If the main shaft of the gyroscope is precession at angular velocity ω under the action of external torque M, the terminal linear velocity of the angular momentum vector H is:
v=ω×H
According to the moment of momentum theorem, the angular momentum H vector terminal velocity v should be equal to the added external moment M, the expression is:
M=ω×H
If the three are perpendicular to each other, the formula can be written as:
M=ω · H
To wit:
ωZ=MY/H
ωY=-MZ/H
It can be seen that under the action of the external torque, the main axis of the gyroscope will produce precession, and the precession direction is determined by the right hand rule. The precession angular velocity is proportional to the external torque and inversely proportional to the angular momentum. Among them, only the external torque component that is perpendicular to the angular momentum H can cause the precession of the gyroscope, and the precession of the gyroscope immediately occurs when the external torque is added to the gyroscope, and the precession of the gyroscope immediately stops when the external torque is removed. Therefore, it can be considered that the precession of the gyroscope is "inertially free". The precession of the gyroscope is based on Newton's theorem. Therefore, the rate of change of the angular momentum of the gyroscope under the action of the external torque is the rate of change of the relative inertial space, so the precession of the main shaft of the gyroscope is relative to the inertial space and is an absolute motion.
Axial rigidity
When the MEMS gyroscope rotor rotates at high speed with angular momentum, if there is no external torque, no matter how the base tilts or wobbles, its main shaft will always remain in the original direction, which is called the fixed axis of the gyroscope. Even if the sudden impact can be understood as giving the gyroscope a moment of impulse, the spindle still remains in the original spatial orientation, which is the nutation of the gyroscope. This impact resistance of the gyroscope is the stability of the gyroscope. The moment of momentum theorem for the axiality of a gyroscope can be understood as saying that if the external moment acting on the gyroscope is zero, then the velocity at the end of the angular momentum is also zero.
It follows that angular momentum changes neither magnitude nor direction in inertial space. Because the direction of angular momentum is consistent with the main axis of the gyroscope, if the main axis always points to a certain direction in space, it will always point to that direction in the future, which is why the gyroscope has a fixed axis. Its stability can also be determined by using the moment of momentum theorem.
Since the moment M is the effect of the pulse, dt approaches zero, so dH also approaches zero, indicating that there is no significant change in angular momentum, that is, the gyroscope spindle will keep the original direction unchanged. It is found through experiments that the greater the angular momentum, the better the stability of the gyroscope.
Conclusion
Through this article, we have learned two characteristics of MEMS gyroscope, through which it can play a role. Ericco specializes in the development of one -, two - and three-axis MEMS gyroscopes. For example, ER-MG2-50/100 has bias instability of 0.01 to 0.02°/hr and angular random walks of 0.0025 to 0.005°/√hr. The ER-2MG-06 is a high-performance two-axis MEMS gyroscope with bias instability of 0.1º/h. The ER-3MG-301 is a high-precision three-axis MEMS gyroscope whose main features are miniaturization and low power consumption.
If you are interested in MEMS gyro, please contact us.
